
どんな情報を渡せば良いんだろう。。
片っ端から渡して色々と試せばいいんだろうか。。
こんにちは、古賀です!
本記事は、
はてな
「Python機械学習でホームラン数を予測する」のデータ分析編
です!
機械学習をするために「データ」を取ってきた後は、
そのデータを分析して、機械に渡すための材料を選ぶ必要があります。
材料選びを間違えると、正しく「ホームラン数」を予測することができません。
正しく「ホームラン数」を予測できるように「データ分析」の基本を学びましょう!
前回の続きになりますので、
前回の記事を読まれていない方はこちらをご覧ください!
-

-
Python機械学習「ホームラン数予測②」データ収集「WEBスクレイピング」編!
PythonのプログラミングでWEBサイトの情報を取ってきたいけど、 どうやってやればいいんだろう。。 CSVデータに出力したいんだけど。。 こんにちは、古賀です! &nb ...
続きを見る
また、実行環境は「JupyterLab」を使っていきますので、
「JupyterLab」の記事を読まれていない方は、こちらもご確認ください!
-

-
JupyterLabとは?Python実行環境「JupyterLab」の概要と基本的な使い方!
Pythonの実行環境「JupyterLab」が起動できるところまできたけど、 どういう風に使っていけばいいんだろう?? そもそも「JupyterLab」ってなんだ?? こ ...
続きを見る
自己紹介が遅れましたが、
わたしは大学卒業後、上場IT企業に就職し、プログラマー、システムエンジニアとして
約10年間働いておりまして、その後は様々な活動をしております。
プロフィールの詳細はこちらです。
-

-
プロフィール
こんにちは、古賀正雄です。 簡単ではありますが、こちらのページで自己紹介とこのブログについてお話します。 高校時代 学生時代は主に野球をしていました。 進学先の高校も野球で選びました。 ...
続きを見る
※YouTubeに同内容を公開しております。
Python機械学習「データ分析」の概要
前回の記事で、WEBサイトから「2020年のプロ野球データ」をCSVファイルに出力しました。
今回はそのデータを使って、「ホームラン数」と関連性が高い項目を調べて、
「説明変数(特徴量)」を作成します。
用語のおさらいですが「説明変数(特徴量)」は、
予測するためのデータ「試合数」や「打席数」、「ヒット数」といった項目です。
この「説明変数(特徴量)」が適切でないと、
予測精度が低くなってしまうので、
ホームランを予測する際に必要のないデータは省いて、
ホームラン数を予測する際に関連性のあるデータだけを渡す必要があります。
「ホームランと関連性の高いデータをどのように調べるか?」
についてですが、「相関係数」を使います。
「相関係数」のおさらいですが、
「-1~1」を取る値のことで、
「-1」に近ければ負の相関があると言って、片方の値が小さければもう片方の数値が大きくなります。
逆に「1」に近ければ正の相関があると言って、片方の値が大きければもう片方の数値も大きくなります。
相関係数が「0」付近であれば、ホームランの数には影響しないデータなので、
「説明変数(特徴量)」からは外すようにします。
野球に詳しい方は、
「どの項目がホームラン数と相関が強いか?」
予想してみてください!
具体的な手順としては、
- プロ野球データを保存したCSVデータを読み込む
- データを巨人と11球団のデータに分ける
- ホームラン数と各項目の相関係数を調べる
- どのデータを説明変数(特徴量)とするか選ぶ
です!
Python機械学習「データ分析」をしてみる!

今回のコード全体です。
今からこのコードを1から説明していきます!
途中、分析用に他のコードも書いていきます!
# 表形式データを扱うライブラリ
import pandas as pd
# CSVデータ読み込み
df = pd.read_csv('playerData.csv', sep = ',')
# 巨人以外の11球団データを抽出
df11 = df[df['チーム'] != '巨人']
# 巨人のデータ
df_g = df[df['チーム'] == '巨人']
# 本塁打との相関係数をDataFrameとして変数に保存
df_homerun = pd.DataFrame(df11.corr()['本塁打'])
# 相関係数「0.8」以上の項目名を抽出
X_columns = df_homerun[df_homerun['本塁打'] >= 0.8].index.tolist()
# 本塁打は目的変数のため除外
X_columns.remove('本塁打')
# 説明変数と目的変数をセット
X = df11[X_columns]
y = df11['本塁打']
CSVファイルの読み込み
まずは、前回ファイル出力した「2020年プロ野球データ」を保存しているCSVファイルを読み込みます。
# 表形式データを扱うライブラリ
import pandas as pd
# CSVデータ読み込み
df = pd.read_csv('playerData.csv', sep = ',')
1行目は前回もお話しましたが、表形式データを扱うためのライブラリ「Pandas」を宣言しています。
2行目で前回出力したCSVファイルを読み込んでいます。
列の項目名を変えたり、読み込むデータのデータ型を指定できたりと、
色々とオプションがあるのですが、
今回は単純に「ファイル名」と「区切り文字(CSVなのでカンマ)」を指定して、
CSVファイルを読み込みます。
読み込んだ結果は表形式データ「DataFrame」型で変数に格納しています。
前回もお話した「type」関数を使って確認してみると、
# データ型確認 print(type(df)) 結果 <class 'pandas.core.frame.DataFrame'>
「DataFrame」型だということが確認できます。
読み込んだデータを色々と確認してみましょう。
まず読み込んだ「項目名」と「データ型」を「DataFrame変数.dtypes」で確認できます。
実行結果を確認すると、こんな感じです。
# 項目名とデータ型 print(df.dtypes) 結果 順位 int64 選手名 object チーム object 打率 float64 試合 int64 打席数 int64 打数 int64 得点 int64 安打 int64 二塁打 int64 三塁打 int64 本塁打 int64 塁打 int64 打点 int64 盗塁 int64 盗塁刺 int64 犠打 int64 犠飛 int64 四球 int64 敬遠 int64 死球 int64 三振 int64 併殺打 int64 出塁率 float64 長打率 float64 dtype: object
続いて「データ数」と「項目数」を「DataFrame変数.shape」で確認できます。
# データ数と項目数確認 print(df.shape) 結果 (328, 25)
結果を確認すると、「328行のデータがあって、25列の項目がある」ということがわかります。
最後にデータの中身を確認します。
「DataFrame」の変数を直接見てみると、
#データの中身を確認
print(df)
結果
順位 選手名 チーム 打率 試合 打席数 打数 得点 安打 二塁打 ... 盗塁刺 犠打 犠飛 \
0 1 鈴木 大地 楽天 0.297 119 541 474 71 141 27 ... 3 12 3
1 2 大島 洋平 中日 0.316 118 525 462 58 146 21 ... 8 9 3
2 3 浅村 栄斗 楽天 0.282 119 524 429 71 121 25 ... 1 0 2
3 4 西川 遥輝 日本ハム 0.307 114 518 417 82 128 16 ... 7 4 3
4 5 柳田 悠岐 ソフトバンク 0.341 118 511 425 89 145 23 ... 2 0 3
.. ... ... ... ... ... ... ... .. ... ... ... ... .. ..
323 321 山崎 勝己 オリックス 0.000 2 1 1 0 0 0 ... 0 0 0
324 321 吉田 裕太 ロッテ 0.000 1 1 0 0 0 0 ... 0 1 0
325 321 加藤 脩平 巨人 0.000 1 1 1 0 0 0 ... 0 0 0
326 327 白崎 浩之 オリックス 0.000 3 0 0 1 0 0 ... 0 0 0
327 327 細谷 圭 ロッテ 0.000 1 0 0 0 0 0 ... 0 0 0
四球 敬遠 死球 三振 併殺打 出塁率 長打率
0 46 0 6 57 17 0.365 0.384
1 47 3 4 51 5 0.382 0.381
2 89 2 4 108 15 0.408 0.564
3 92 1 2 84 5 0.432 0.396
4 82 8 1 103 2 0.446 0.616
.. .. .. .. ... ... ... ...
323 0 0 0 0 0 0.000 0.000
324 0 0 0 0 0 0.000 0.000
325 0 0 0 1 0 0.000 0.000
326 0 0 0 0 0 0.000 0.000
327 0 0 0 0 0 0.000 0.000
[328 rows x 25 columns]
前回取ってきたプロ野球選手のデータが読み込めています。
これで今回の第一段階クリアです!
データを巨人と11球団のデータに分ける
読み込んだプロ野球選手データですが、現状だと全12球団のデータがひとまとまりになっています。
改めて確認ですが、今回のゴールは、
「11球団のデータを使って機械学習させて、巨人の選手のホームラン数を当てる!」
ことです。
なので、機械学習を終えるまで、一旦巨人のデータは別に退避させておいて、
「教師データ」となる「11球団のデータ」と分けておく必要があります。
おさらいになりますが「教師データ」は機械学習するためのデータのことです。
以下のように「11球団のデータ」と「巨人のデータ」を別々の変数にセットします。
# 巨人以外の11球団データを抽出 df11 = df[df['チーム'] != '巨人'] # 巨人のデータ df_g = df[df['チーム'] == '巨人']
このように書くことで、それぞれ「df11」、「df_g」の変数にデータを分けることができます。
もう少し「DataFrame」の操作を細かく説明しておきます。
先程、CSVファイルから読み込んだデータの中身を確認しましたが、
一部の項目だけ確認したい場合は「df[列名]」とすることで、指定した項目だけ確認することができます。
「チーム」のみ確認したい場合は、このような感じです。
# チーム名のみ表示
print(df['チーム'])
結果
0 楽天
1 中日
2 楽天
3 日本ハム
4 ソフトバンク
...
323 オリックス
324 ロッテ
325 巨人
326 オリックス
327 ロッテ
Name: チーム, Length: 328, dtype: object
ちなみに「1列のみ」、「1行のみ」取り出したデータは、
「DataFrame」型ではなく「Series」型と呼ばれるので覚えておきましょう!
複数列指定したい場合は、「df[[列名,列名,・・・,列名]]」
と列指定を配列型とすることで、複数列のデータを確認できます。
※配列については、前回の記事で説明しています。
「選手名」と「チーム」を指定すると、このような感じです。
# 選手名、チームを表示
print(df[['選手名','チーム']])
結果
選手名 チーム
0 鈴木 大地 楽天
1 大島 洋平 中日
2 浅村 栄斗 楽天
3 西川 遥輝 日本ハム
4 柳田 悠岐 ソフトバンク
.. ... ...
323 山崎 勝己 オリックス
324 吉田 裕太 ロッテ
325 加藤 脩平 巨人
326 白崎 浩之 オリックス
327 細谷 圭 ロッテ
[328 rows x 2 columns]
これを踏まえて上で、巨人以外のデータを取り出したい場合を考えます。
まず各行データが「巨人以外」か調べたい時は、
# 巨人以外の行データを調べる
print(df['チーム'] != '巨人')
結果
0 True
1 True
2 True
3 True
4 True
...
323 True
324 True
325 False
326 True
327 True
Name: チーム, Length: 328, dtype: bool
とこのようにすることで、「巨人以外」であれば「True」が返ってきます。
そして「df[ ]」の中に、この結果を入れるとファルターの役割を果たしてくれるので、
# 巨人以外の11球団データを抽出
print(df[df['チーム'] != '巨人'])
結果
順位 選手名 チーム 打率 試合 打席数 打数 得点 安打 二塁打 ... 盗塁刺 犠打 犠飛 \
0 1 鈴木 大地 楽天 0.297 119 541 474 71 141 27 ... 3 12 3
1 2 大島 洋平 中日 0.316 118 525 462 58 146 21 ... 8 9 3
2 3 浅村 栄斗 楽天 0.282 119 524 429 71 121 25 ... 1 0 2
3 4 西川 遥輝 日本ハム 0.307 114 518 417 82 128 16 ... 7 4 3
4 5 柳田 悠岐 ソフトバンク 0.341 118 511 425 89 145 23 ... 2 0 3
.. ... ... ... ... ... ... ... .. ... ... ... ... .. ..
322 321 白濱 裕太 広島 0.000 2 1 1 0 0 0 ... 0 0 0
323 321 山崎 勝己 オリックス 0.000 2 1 1 0 0 0 ... 0 0 0
324 321 吉田 裕太 ロッテ 0.000 1 1 0 0 0 0 ... 0 1 0
326 327 白崎 浩之 オリックス 0.000 3 0 0 1 0 0 ... 0 0 0
327 327 細谷 圭 ロッテ 0.000 1 0 0 0 0 0 ... 0 0 0
四球 敬遠 死球 三振 併殺打 出塁率 長打率
0 46 0 6 57 17 0.365 0.384
1 47 3 4 51 5 0.382 0.381
2 89 2 4 108 15 0.408 0.564
3 92 1 2 84 5 0.432 0.396
4 82 8 1 103 2 0.446 0.616
.. .. .. .. ... ... ... ...
322 0 0 0 0 0 0.000 0.000
323 0 0 0 0 0 0.000 0.000
324 0 0 0 0 0 0.000 0.000
326 0 0 0 0 0 0.000 0.000
327 0 0 0 0 0 0.000 0.000
[301 rows x 25 columns]
「巨人以外」のデータを抽出することができます。
これを別の変数「df11」に格納しています。
「巨人のみ」を取り出したい場合は、条件文を逆にするだけです。
これで、「11球団」のデータ、「巨人」のデータの2つに分けることができました。
ホームラン数との相関係数を調べる
ようやく今回の本題に入ります。
ホームラン数と各項目の相関の強弱を調べていきます。
相関の強弱を調べる方法はいくつかありますが、その中の1つ「散布図」を見ることで確認することができます。
下記のように書くと、「打席数」と「ホームラン数」の散布図を確認できます。
グラフを表示したい場合は「matplotlib」ライブラリを使います。
散布図を表示させるための「scatter」関数の引数に、
11球団データをセットしている変数から「打席数」と「本塁打」のデータを列名を指定して渡しています。
# グラフ可視化ランブラリ from matplotlib import pyplot as plt # JupyterLabでグラフを表示させるための記述 %matplotlib inline # 散布図 plt.scatter(x = df11['打席数'], y = df11['本塁打']) # グラフ表示 plt.show()
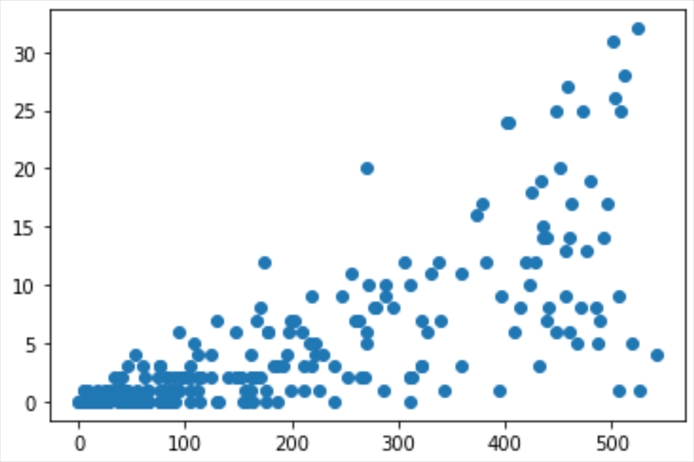
グラフを見ると、こんな感じです。
散布図は数学の授業で習ったと思いますが、綺麗な右肩あがりになっていれば相関が強いと言えます。
逆に右肩下がりになっていると、負の相関が強いと言えて、
各点がバラバラだと相関がないと判断できます。
このグラフを見ると、綺麗な右肩あがりではないですが、多少の相関があると言えそうです。
野球の知識の目線から考えても、打席数が多ければ、当然ホームランの数も増えるので、
相関があることは当然です。
ただ、このように各項目とホームラン数との相関を1つずつ散布図で確認するとなると、
ちょっと大変です。しかも、目視で相関があるかないか判断する必要があります。
そこで、冒頭に説明した「相関係数」を調べて、相関の強弱を数値で表しましょう!
「corr」という関数を使う事で、各項目の相関係数を一気に確認することができるので便利です。
実行してみると、
# 各項目間の相関係数
print(df11.corr())
結果
順位 打率 試合 打席数 打数 得点 安打 \
順位 1.000000 -0.407034 -0.934417 -0.934977 -0.935255 -0.860108 -0.900221
打率 -0.407034 1.000000 0.366004 0.388513 0.389626 0.390378 0.424232
試合 -0.934417 0.366004 1.000000 0.922792 0.921952 0.868782 0.889536
打席数 -0.934977 0.388513 0.922792 1.000000 0.998208 0.944063 0.983963
打数 -0.935255 0.389626 0.921952 0.998208 1.000000 0.936799 0.984953
得点 -0.860108 0.390378 0.868782 0.944063 0.936799 1.000000 0.950077
安打 -0.900221 0.424232 0.889536 0.983963 0.984953 0.950077 1.000000
二塁打 -0.843887 0.395273 0.828466 0.924497 0.923328 0.892092 0.940341
三塁打 -0.495558 0.244762 0.493597 0.536260 0.542186 0.555815 0.552179
本塁打 -0.678139 0.294984 0.661433 0.764071 0.758635 0.769061 0.754315
塁打 -0.882355 0.408799 0.868877 0.971135 0.970267 0.948251 0.980858
打点 -0.818896 0.361392 0.809607 0.910505 0.906890 0.868322 0.903396
盗塁 -0.423355 0.197726 0.451352 0.450689 0.443318 0.549285 0.457709
盗塁刺 -0.537767 0.245504 0.561521 0.576515 0.573605 0.630112 0.574919
犠打 -0.403369 0.086484 0.427915 0.353001 0.344342 0.312046 0.292700
犠飛 -0.649831 0.236060 0.647798 0.708958 0.702771 0.636142 0.678164
四球 -0.811754 0.349452 0.803113 0.900199 0.875558 0.896145 0.880956
敬遠 -0.461168 0.240239 0.469577 0.544601 0.532487 0.561683 0.581294
死球 -0.597036 0.245212 0.587231 0.627717 0.612601 0.610905 0.592740
三振 -0.883647 0.335602 0.865667 0.919998 0.917096 0.859531 0.874721
併殺打 -0.737975 0.284621 0.710598 0.794022 0.797227 0.696335 0.776520
出塁率 -0.497143 0.925239 0.448031 0.457353 0.448859 0.462939 0.473222
長打率 -0.478139 0.843386 0.406216 0.462812 0.462631 0.467340 0.486966
二塁打 三塁打 本塁打 ... 盗塁刺 犠打 犠飛 \
順位 -0.843887 -0.495558 -0.678139 ... -0.537767 -0.403369 -0.649831
打率 0.395273 0.244762 0.294984 ... 0.245504 0.086484 0.236060
試合 0.828466 0.493597 0.661433 ... 0.561521 0.427915 0.647798
打席数 0.924497 0.536260 0.764071 ... 0.576515 0.353001 0.708958
打数 0.923328 0.542186 0.758635 ... 0.573605 0.344342 0.702771
得点 0.892092 0.555815 0.769061 ... 0.630112 0.312046 0.636142
安打 0.940341 0.552179 0.754315 ... 0.574919 0.292700 0.678164
二塁打 1.000000 0.449028 0.745479 ... 0.473280 0.248414 0.641879
三塁打 0.449028 1.000000 0.274924 ... 0.509776 0.373842 0.276446
本塁打 0.745479 0.274924 1.000000 ... 0.229921 -0.033971 0.575423
塁打 0.943711 0.519432 0.864265 ... 0.504151 0.217994 0.680445
打点 0.884380 0.384544 0.923236 ... 0.354050 0.104097 0.723225
盗塁 0.354910 0.547908 0.138545 ... 0.724176 0.397880 0.236131
盗塁刺 0.473280 0.509776 0.229921 ... 1.000000 0.456809 0.314738
犠打 0.248414 0.373842 -0.033971 ... 0.456809 1.000000 0.187193
犠飛 0.641879 0.276446 0.575423 ... 0.314738 0.187193 1.000000
四球 0.848303 0.410133 0.769491 ... 0.489593 0.205390 0.651867
敬遠 0.561524 0.237957 0.599605 ... 0.291735 -0.033799 0.357820
死球 0.558686 0.261623 0.551520 ... 0.348905 0.195932 0.438145
三振 0.840638 0.499156 0.802282 ... 0.483813 0.290622 0.626104
併殺打 0.757420 0.201916 0.733118 ... 0.298469 0.135071 0.650338
出塁率 0.447319 0.243483 0.361484 ... 0.290539 0.107659 0.288040
長打率 0.485034 0.265860 0.510274 ... 0.190801 0.022464 0.295525
四球 敬遠 死球 三振 併殺打 出塁率 長打率
順位 -0.811754 -0.461168 -0.597036 -0.883647 -0.737975 -0.497143 -0.478139
打率 0.349452 0.240239 0.245212 0.335602 0.284621 0.925239 0.843386
試合 0.803113 0.469577 0.587231 0.865667 0.710598 0.448031 0.406216
打席数 0.900199 0.544601 0.627717 0.919998 0.794022 0.457353 0.462812
打数 0.875558 0.532487 0.612601 0.917096 0.797227 0.448859 0.462631
得点 0.896145 0.561683 0.610905 0.859531 0.696335 0.462939 0.467340
安打 0.880956 0.581294 0.592740 0.874721 0.776520 0.473222 0.486966
二塁打 0.848303 0.561524 0.558686 0.840638 0.757420 0.447319 0.485034
三塁打 0.410133 0.237957 0.261623 0.499156 0.201916 0.243483 0.265860
本塁打 0.769491 0.599605 0.551520 0.802282 0.733118 0.361484 0.510274
塁打 0.894044 0.615646 0.609416 0.902293 0.798908 0.465056 0.522403
打点 0.869742 0.603727 0.601443 0.885161 0.828535 0.426280 0.508422
盗塁 0.415637 0.159772 0.251690 0.401064 0.146354 0.234763 0.147142
盗塁刺 0.489593 0.291735 0.348905 0.483813 0.298469 0.290539 0.190801
犠打 0.205390 -0.033799 0.195932 0.290622 0.135071 0.107659 0.022464
犠飛 0.651867 0.357820 0.438145 0.626104 0.650338 0.288040 0.295525
四球 1.000000 0.604869 0.601912 0.848648 0.702899 0.475188 0.439219
敬遠 0.604869 1.000000 0.483248 0.468371 0.434543 0.295121 0.322468
死球 0.601912 0.483248 1.000000 0.560026 0.504295 0.350018 0.323654
三振 0.848648 0.468371 0.560026 1.000000 0.728055 0.417665 0.458401
併殺打 0.702899 0.434543 0.504295 0.728055 1.000000 0.341181 0.393600
出塁率 0.475188 0.295121 0.350018 0.417665 0.341181 1.000000 0.824454
長打率 0.439219 0.322468 0.323654 0.458401 0.393600 0.824454 1.000000
[23 rows x 23 columns]
こんな感じです。
「corr」を使うと、全ての項目同士の相関係数が見れます。
今回欲しい情報は「本塁打」と「各項目」の相関係数ですので、上記の実行結果に対して「本塁打」お列を指定しましょう。
# 本塁打と各項目間の相関係数 print(df11.corr()['本塁打']) 結果 順位 -0.678139 打率 0.294984 試合 0.661433 打席数 0.764071 打数 0.758635 得点 0.769061 安打 0.754315 二塁打 0.745479 三塁打 0.274924 本塁打 1.000000 塁打 0.864265 打点 0.923236 盗塁 0.138545 盗塁刺 0.229921 犠打 -0.033971 犠飛 0.575423 四球 0.769491 敬遠 0.599605 死球 0.551520 三振 0.802282 併殺打 0.733118 出塁率 0.361484 長打率 0.510274 Name: 本塁打, dtype: float64
これで「各項目」と「本塁打」の相関係数を確認することができました。
これを見ると、「塁打」や「打点」に正の強い相関があって、
「盗塁」や「犠打」といった項目には相関がなさそうです。
「順位」に負のやや強い相関がありますが、これはWEBサイト上の行番号なので無視してよさそうです。
「本塁打」の項目が「1.0」と表示されていますが、これは本塁打同士の相関なので当たり前ですね。
野球に詳しい方であれば、「三振」や「併殺」が「本塁打」と相関が強いことに違和感を感じると思います。
詳しくない方向けに簡単に説明すると、「三振」や「併殺」は打者にとってはマイナスの数値です。
それが「本塁打」と相関が強いので、以外な結果ですね。
三振や併殺を恐れずにしっかりスイングしている証拠なのかもしれませんが、
このあたりが「データ分析」の面白いところかなと思います。
説明変数(特徴量)を選ぶ
相関係数を調べ終えたところで、相関が強い項目を選んで「説明変数(特徴量)」を作成しましょう。
一般的に相関係数が「0.7」以上だと「相関がかなり強い」と判断されますが、
とりあえず今回は、もう1つ上の「0.8」以上の項目を「説明変数(特徴量)」としましょう。
相関係数が「0.8」以上の項目は先程の結果を見ると、
「塁打」、「打点」、「三振」と「本塁打」自身です。
「説明変数(特徴量)」の作成を直接列名を書き込んで、
# 説明変数を直接列名を指定 print(df11[['塁打', '打点', '三振']]) 結果 塁打 打点 三振 0 182 55 57 1 176 30 51 2 242 104 108 3 165 38 84 4 262 84 103 .. ... ... ... 322 0 0 0 323 0 0 0 324 0 0 0 326 0 0 0 327 0 0 0
としても良いのですが、せっかくなのでもう少しかっこよく書いていきましょう!
# 本塁打との相関係数をDataFrameとして変数に保存
df_homerun = pd.DataFrame(df11.corr()['本塁打'])
# 相関係数「0.8」以上の項目名を抽出
X_columns = df_homerun[df_homerun['本塁打'] >= 0.8].index.tolist()
# 本塁打は目的変数のため除外
X_columns.remove('本塁打')
# 説明変数と目的変数をセット
X = df11[X_columns]
y = df11['本塁打']
これで今回のゴール「説明変数(特徴量)」の作成が完了です。
1行目で先程確認した「各項目」と「本塁打」との相関係数の結果を「DataFrame」型として、
変数にセットしています。
2行目で相関係数が「0.8」以上の項目名を配列型で抽出して、変数に格納しているのですが、
まず、
# 相関係数が「0.8」以上のデータ
print(df_homerun[df_homerun['本塁打'] >= 0.8])
結果
本塁打
本塁打 1.000000
塁打 0.864265
打点 0.923236
三振 0.802282
で、相関係数が「0.8」以上の行データを取り出しています。
この書き方は先程「11球団」のデータと「巨人」のデータを分けた時と一緒です。
欲しい情報は結果の左側に表示されている項目名です。
この左側に表示されている情報は「インデックス」と呼びます。
この「インデックス」情報を取得するためには「DataFrame変数.index」で取得できて、
さらに配列型とするためには「tolist()」を加えます。
# 相関係数0.8以上のインデックス項目名を配列型で取得 print(df_homerun[df_homerun['本塁打'] >= 0.8].index.tolist()) 結果 ['本塁打', '塁打', '打点', '三振']
後は「本塁打」は「目的変数」なので、この配列型変数から除外する必要があります。
3行目の「remove('本塁打')」で除外しています。
これで「説明変数(特徴量)」の項目名を取得できたので、
最後「説明変数(特徴量)」の変数「X(複数データなので大文字にする風習があります)」に相関の強いデータを、
「目的変数」の変数「y」に「本塁打」データをセットしています。
# 説明変数と目的変数をセット
X = df11[X_columns]
y = df11['本塁打']
print(X)
print(y)
結果
塁打 打点 三振
0 182 55 57
1 176 30 51
2 242 104 108
3 165 38 84
4 262 84 103
.. ... ... ...
322 0 0 0
323 0 0 0
324 0 0 0
326 0 0 0
327 0 0 0
[301 rows x 3 columns]
0 4
1 1
2 32
3 5
4 28
..
322 0
323 0
324 0
326 0
327 0
Name: 本塁打, Length: 301, dtype: int64
次回はこの「X」と「y」を使って、機械学習をします!
最後に今回のコード全体をもう一度見てみましょう!
# 表形式データを扱うライブラリ
import pandas as pd
# CSVデータ読み込み
df = pd.read_csv('playerData.csv', sep = ',')
# 巨人以外の11球団データを抽出
df11 = df[df['チーム'] != '巨人']
# 巨人のデータ
df_g = df[df['チーム'] == '巨人']
# 本塁打との相関係数をDataFrameとして変数に保存
df_homerun = pd.DataFrame(df11.corr()['本塁打'])
# 相関係数「0.8」以上の項目名を抽出
X_columns = df_homerun[df_homerun['本塁打'] >= 0.8].index.tolist()
# 本塁打は目的変数のため除外
X_columns.remove('本塁打')
# 説明変数と目的変数をセット
X = df11[X_columns]
y = df11['本塁打']
まとめ:Python機械学習「データ分析」
ここまでの話をまとめます。
まとめ
今回は「ホームラン数」を予測するためのデータ「説明変数(特徴量)」を相関係数を使って作成した!
今回やったことは、
- プロ野球データを保存したCSVデータを読み込む
- データを巨人と11球団のデータに分ける
- ホームラン数と各項目の相関係数を調べる
- 相関係数が「0.8」以上の項目を説明変数(特徴量)とした
機械学習に必要な「説明変数(特徴量)」と「目的変数」のデータを用意することができた!
今回は「相関係数」を調べることで、「説明変数(特徴量)」を作成しましたが、
「データ分析」の方法は、課題によって変わってきます。
散布図のグラフを確認したように、様々なグラフを作成して分析する場合もあれば、
自分で新しい項目を作成する方法もあります。
今回の「説明変数(特徴量)」の作成が正しいかどうかは次回以降でわかります。
(※野球に詳しい方であれば、「何を渡すのが一番良いか?」わかると思いますが。。)
もし結果が悪い場合は「説明変数(特徴量)」の見直しが必要です。
次回は「モデル作成・モデル評価」編です!
今回作成した「説明変数(特徴量)」と「目的変数」を機械に渡して、
「予測モデル」を作成します!
※次の記事へ
-

-
Python機械学習「ホームラン数予測④」モデル作成・モデル評価編!
「機械学習させてAIを作る!」ってなんだか難しそう。。 自分のレベルでもできるのかな。。 こんにちは、古賀です! 本記事は、 はてな 「Python機械学習で ...
続きを見る



